Metric Temporal Logic (MTL) as-a-service
| assets | ||
| mtl | ||
| .gitignore | ||
| .travis.yml | ||
| LICENSE | ||
| README.md | ||
| requirements.txt | ||
| setup.py | ||
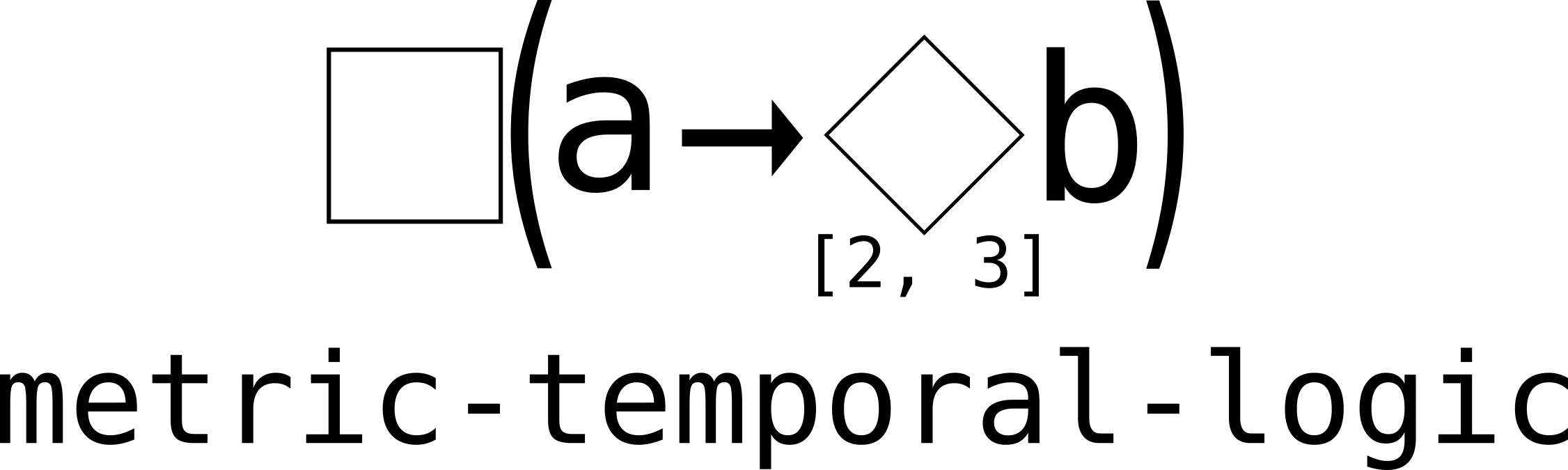
About
Python library for working with Metric Temporal Logic (MTL). Metric Temporal Logic is an extension of Linear Temporal Logic (LTL) for specifying properties over time series (See Alur). Some practical examples are given in the usage.
Installation
$ pip install metric-temporal-logic
Usage
To begin, we import mtl.
import mtl
Propositional logic (using parse api)
# - Lowercase strings denote atomic predicates.
phi0 = mtl.parse('atomicpred')
# - Binary operators need to be surrounded by parens.
phi1 = mtl.parse('((a & b & c) | d | e)')
phi2 = mtl.parse('(a -> b) & (~a -> c)')
phi3 = mtl.parse('(a -> b -> c)')
phi4 = mtl.parse('(a <-> b <-> c)')
phi5 = mtl.parse('(x ^ y ^ z)')
# - Unary operators (negation)
phi6 = mtl.parse('~a')
phi7 = mtl.parse('~(a)')
Propositional logic (using python syntax)
a, b = mtl.parse('a'), mtl.parse('b')
phi0 = ~a
phi1 = a & b
phi2 = a | b
# TODO: add
phi3 = a ^ b
phi4 = a.iff(b)
phi5 = a.implies(b)
Modal Logic (parser api)
# Eventually `x` will hold.
phi1 = mtl.parse('F x')
# `x & y` will always hold.
phi2 = mtl.parse('G(x & y)')
# `x` holds until `y` holds.
# Note that since `U` is binary, it requires parens.
phi3 = mtl.parse('(x U y)')
# Weak until (`y` never has to hold).
phi4 = mtl.parse('(x W y)')
# Whenever `x` holds, then `y` holds in the next two time units.
phi5 = mtl.parse('G(x -> F[0, 2] y)')
# We also support timed until.
phi6 = mtl.parse('(a U[0, 2] b)')
# Finally, if time is discretized, we also support the next operator.
# Thus, LTL can also be modeled.
# `a` holds in two time steps.
phi7 = mtl.parse('XX a')
Modal Logic (using python syntax)
a, b = mtl.parse('a'), mtl.parse('b')
# Eventually `a` will hold.
phi1 = a.eventually()
# `a & b` will always hold.
phi2 = (a & b).always()
# `a` until `b`
phi3 = a.until()
# `a` weak until `b`
phi4 = a.weak_until(b)
# Whenever `a` holds, then `b` holds in the next two time units.
phi5 = (a.implies(b.eventually(lo=0, hi=2))).always()
# We also support timed until.
phi6 = a.timed_until(b, lo=0, hi=2)
# `a` holds in two time steps.
phi7 = a >> 2
Boolean Evaluation
# Assumes piece wise constant interpolation.
data = {
'a': [(0, True), (1, False), (3, False)]
'b': [(0, False), (0.2, True), (4, False)]
}
phi = mtl.parse('F(a | b)')
print(phi(data, quantitative=False))
# output: True
# Evaluate at t=3
print(phi(data, t=3, quantitative=False))
# output: False
# Evaluate with discrete time
phi = mtl.parse('X b')
print(phi(data, dt=0.2, quantitative=False))
# output: True
Quantitative Evaluate
# Assumes piece wise constant interpolation.
data = {
'a': [(0, 100), (1, -1), (3, -2)]
'b': [(0, 20), (0.2, 2), (4, -10)]
}
phi = mtl.parse('F(a | b)')
print(phi(data))
# output: 100
# Evaluate at t=3
print(phi(data, t=3))
# output: 2
# Evaluate with discrete time
phi = mtl.parse('X b')
print(phi(data, dt=0.2))
# output: 2
Utilities
import mtl
from mtl import utils
print(utils.scope(mtl.parse('XX a'), dt=0.1))
# output: 0.2
print(utils.discretize(mtl.parse('F[0, 0.2] a'), dt=0.1))
# output: (a | X a | XX a)
